Định lý pytago
Trong hình học, định lý Py-ta-go chỉ mối liên hệ căn bản trong hình học Euclid giữa 3 cạnh của một tam giác vuông.

Nhà toán học hy lạp cổ đại Pythagoras
Định lý Pythagoras:
Trong một tam giác vuông, bình phương của cạnh huyền sẽ bằng tổng 2 bình phương của hai cạnh góc vuông. Định lý này áp dụng đúng cả trong trường hợp tam giác vuông cân.
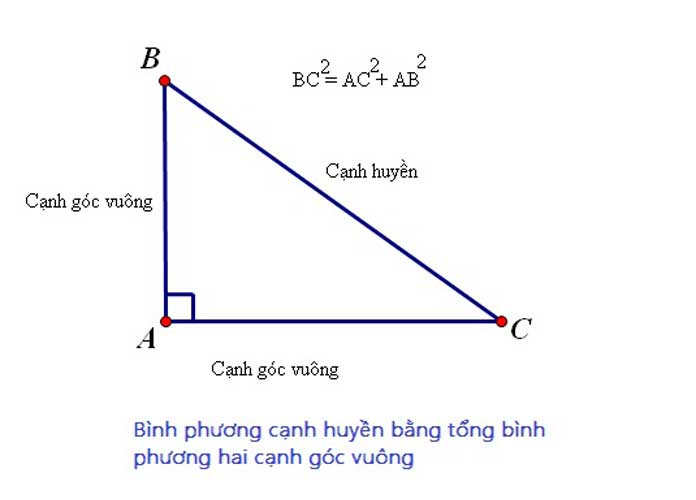
Định lý pytago
Chẳng hạn: Với tam giác ABC vuông tại A.
Ta có: BC² = AB² + AC² hay a² = b² + c² (ký hiệu: a = BC, b = AC, c = AB).
Ví dụ: Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Tính độ dài cạnh BC.
Lời giải:
Do tam giác ABC vuông tại A áp dụng định lý Pythagore, ta có:
BC² = AB² + AC² = 6² + 8² = 36 + 64 = 100.
Do đó : BC= √100=10
Vậy BC = 10 cm.
Tham khảo: 5 bài tập pháp luân công
Phát biểu định lý Pythagore đảo như sau:
Nếu một tam giác thỏa mãn bình phương của một cạnh bằng tổng các bình phương của 2 cạnh còn lại thì tam giác đó là tam giác vuông.
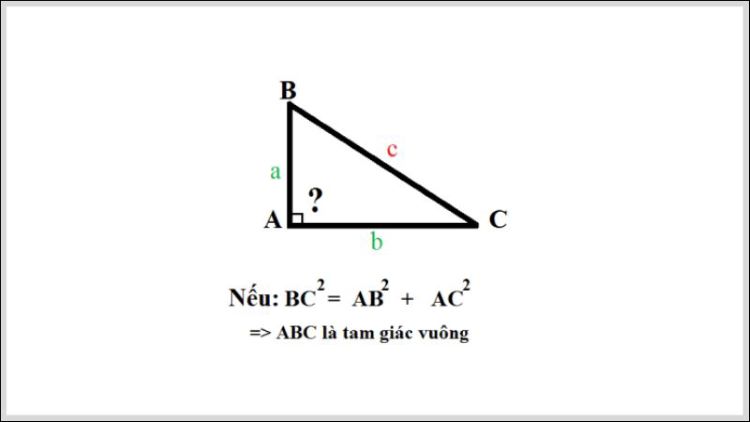
Định lý pytago đảo
Ví dụ: Cho tam giác ABC.
Nếu BC² = AB² + AC² hay a² = b² + c² (trong đó a = BC, b = AC, c = AB) thì tam giác ABC là tam giác vuông tại A.
Ví dụ: Cho tam giác CDE có CD = 7 cm, CE = 24 cm và DE = 25 cm. Tam giác CDE có phải là tam giác vuông hay không?
Hướng dẫn giải
Xét tam giác CDE, ta có: DE² = 25² = 625 (cm2)
Mặt khác, CD² +CE² = 7² + 24² = 49 + 576 = 625 cm2)
Suy ra DE² = CD² + CE².
Do đó tam giác CDE vuông tại C (theo định lý Pythagore đảo).
Thông thường, sử dụng định lý Pythagore đảo để nhận biết tam giác có vuông hay không.
Phương pháp:
+ Tính bình phương độ dài 3 cạnh của 1 tam giác.
+ So sánh bình phương của cạnh lớn nhất so với tổng các bình phương của hai cạnh còn lại.
+ Nếu hai kết quả bằng nhau thì kết luận đó là tam giác vuông, cạnh lớn nhất là cạnh huyền.
Ví dụ 1. Cho tam giác ABC vuông tại A. Biết AB = 6 cm và AC = 8 cm. Tính độ dài BC.
Giải:
Áp dụng định lí Pytago trong tam giác vuông ABC, ta có:
BC² = AB² + AC²
⇔ BC² = 6² + 8² = 36 + 64 = 100 = 10²
Vậy BC = 10cm.
Ví dụ 2. Cho tam giác ABC có độ dài AC = 5 cm, BC = 3 cm và AB = 4 cm. Tam giác ABC là tam giác gì?
Giải:
Ta có: AC² = BC² + AB² (vì 5² = 3² + 4²)
Nên tam giác ABC vuông tại B (Áp dụng định lí Pythagore đảo)
Bài 1: Cho tam giác ABC có góc B = 90 độ. Khi đó, hằng đẳng thức đúng là:
A. AB² + BC² = AC²
B. AB² - BC²= AC²
C. AB² + AC² = BC²
D. AB² = AC² + BC²
Lời giải:
Ta có tam giác ABC vuông tại B, theo định lý pytago: AB² + BC² = AC²
Vậy chọn đáp án A.
Bài 2: Cho tam giác ABC vuông cân tại đỉnh A. Tính độ dài cạnh huyền BC biết AB = AC = 2dm
A. BC = 4 dm B. BC = √6 dm C. BC = 8dm D. BC = √8 dm
Lời giải:
Áp dụng định lí pytago ta có: BC² = AB² + AC²
Khi đó ta có: BC =√( AB²+ AC²)= √4+4=√8
Vậy Chọn đáp án D.
Bài 3: Một tam giác vuông có cạnh huyền độ dài bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?
A. 10 cm, 22 cm B. 10 cm, 24 cm C. 12 cm, 24 cm D. 15 cm, 24 cm
Lời giải:
Gọi độ dài các cạnh góc vuông cần tìm lần lượt là x, y (x, y > 0)
Theo định lí Py – ta – go ta có: x² + y² = 262 ⇔ x² + y² = 676 (1)
Theo bài ra ta có: x/y = 5/12=> x=5y/12 (2)
Từ (1) và (2) ta có:
x² + y² = 676
x=5y/12
=> (5y/12)² +y²=676 ⇔ 25y² + 144y²= 97344 ⇔ y² = 576
=> y = 24 => x= 5y/12 = 5.24/12=10
Vậy chọn B.
Bài 4: Cho ∆ABC vuông tại A có AC = 20cm. Kẻ AH vuông góc với đoạn BC. Biết BH = 9cm, HC = 16cm. Tính độ dài cạnh của AB, AH ?
A. AH = 12cm, AB = 15cm
B. AH = 10cm, AB = 15cm
C. AH = 15cm, AB = 12cm
D. AH = 12cm, AB = 13cm
Lời giải:
Ta có: BC = HB + HC = 9 + 16 = 25 (cm)
Xét tam giác ABC vuông tại A, áp dụng định lí Pytago cho tam giác ta có:
BC² = AB² + AC² ⇒ AB² = BC² - AC² = 25² - 20² = 225 ⇒ AB = 15cm
Xét tam giác ABH vuông tại H, áp dụng định lí Pytago ta có:
HB² + HA² = AB² ⇒ AH² = AB² - HB² = 15² - 9² = 144 ⇒ AH = 12cm
Vậy AH = 12cm và AB = 15cm
Chọn đáp án A.
Bài 5: Cho ∆ABC vuông tại B, cho biết BA=12cm, AC= 13cm, tính BC=x=?
A. x = 10cm B. x = 11cm C. x = 8cm D. x = 5cm
Lời giải:
Xét tam giác ABC vuông tại B ta có:
⇒ x² + 12² = 13² ⇒ x² = 13² - 12² = 25
Khi đó: x = 5cm
Chọn đáp án D.