Thể tích khối lập phương
Khối lập phương là một loại khối hình học ba chiều đặc biệt, có các đặc điểm nổi bật:
6 mặt đều là hình vuông
12 cạnh bằng nhau, ký hiệu là “ a”
8 đỉnh, mỗi góc là góc vuông 90°
Khối lập phương là trường hợp đặc biệt của hình hộp chữ nhật, khi chiều dài, chiều rộng và chiều cao bằng nhau. Nhờ đặc điểm này, việc tính toán về khối lập phương trở nên cực kỳ đơn giản.
Một số đặc điểm cần ghi nhớ
Mỗi mặt có diện tích bằng a × a=a²
Diện tích toàn phần: S=6 × a²
Thể tích: V=a³
Tất cả các góc đều là góc vuông
Lịch sử và ý nghĩa khối lập phương
Khối lập phương xuất hiện từ lâu trong toán học và kiến trúc. Trong lịch sử, các nhà toán học cổ đại như Euclid đã nghiên cứu khối lập phương trong các bài toán về hình học không gian.
Ý nghĩa của khối lập phương:
Là nền tảng để học các hình khối phức tạp hơn như hình hộp chữ nhật, hình lăng trụ, hình trụ.
Giúp học sinh làm quen với khái niệm thể tích và đơn vị đo thể tích.
Ứng dụng rộng rãi trong đời sống, từ tính toán khoang chứa, đóng gói sản phẩm, đến xây dựng công trình.
Hình lập phương là gì?
Công thức tính thể tích rất đơn giản:
V=a³
Trong đó:
V: thể tích khối lập phương
a: độ dài cạnh khối lập phương
Ví dụ:
Nếu cạnh khối lập phương là 4 cm, thể tích là:
V=4³ =64 cm³
Nếu cạnh là 2 m, thể tích là:
V=2³ =8 m³
Lưu ý về đơn vị
Nếu đo bằng cm → thể tích ra cm³
Nếu đo bằng m → thể tích ra m³
Nếu đo bằng dm → thể tích ra dm³
Ví dụ minh họa
Ví dụ 1: Bài tập lớp học
Khối lập phương có cạnh dài 5 cm. Tính thể tích.
Giải:
V=a³ =5³ =125 cm³
Như vậy, thể tích của khối lập phương là 125 cm³ .
Ví dụ 2: Ứng dụng thực tế
Một thùng hình lập phương có cạnh 2 m. Tính thể tích.
Giải:
V=a³ =2³ =8 m³
Thùng này chiếm 8 m³ thể tích, có thể dùng để tính lượng nước cần để đổ đầy, hoặc tính khối lượng vật liệu.
Ví dụ 3: Bài tập nâng cao
Một khối lập phương có thể tích 343 cm³ . Tính cạnh khối lập phương.
Giải:
V=a³ → a=∛V=∛343=7 cm
Một số lưu ý khi tính thể tích
Đo đúng cạnh: Sai số khi đo dẫn đến sai thể tích.
Chuyển đổi đơn vị: Nếu cần, chuyển tất cả sang cùng đơn vị trước khi tính.
Áp dụng đúng công thức: Chỉ áp dụng công thức V=a³ cho khối lập phương.
Kiểm tra kết quả: So sánh với bài toán thực tế hoặc ước lượng để tránh nhầm lẫn.
Các bài toán áp dụng
Trong đời sống:
Tính thể tích hộp đựng đồ, thùng hàng.
Tính lượng nước cần đổ đầy bể, hồ chứa.
Trong giáo dục:
Là bài tập cơ bản về hình học 3D.
Giúp học sinh làm quen với khái niệm không gian và đơn vị đo thể tích.
Trong kỹ thuật và xây dựng:
Tính khối lượng vật liệu như bê tông, cát, gạch.
Thiết kế sản phẩm dạng khối lập phương, hộp đựng, khối cơ khí.
Mẹo và checklist khi tính thể tích
Mẹo
Nếu cạnh là số nguyên nhỏ, nhẩm lập phương sẽ nhanh chóng. Ví dụ: 3³ =27, 4³ =64.
Đổi tất cả đơn vị sang cùng loại trước khi tính.
Luôn kiểm tra đơn vị sau khi tính.
Trong thực tế, đo nhiều lần để đảm bảo chính xác.
Checklist nhanh
Đo cạnh chính xác
Chuyển đổi đơn vị nếu cần
Áp dụng công thức V=a³
Kiểm tra kết quả và đơn vị
Áp dụng vào bài tập hoặc thực tế
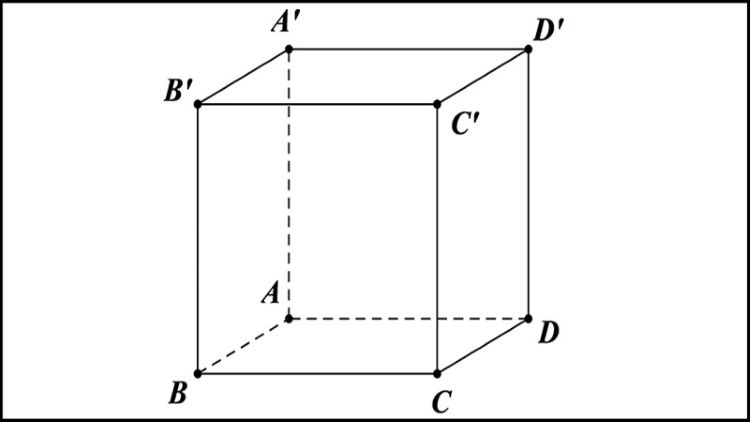Hình lập phương ABCDA'B'C'D'1. Thể tích khối lập phương khác gì hình hộp chữ nhật?
Khối lập phương là hình hộp chữ nhật đặc biệt, có 3 cạnh bằng nhau.
2. Có thể tính thể tích nếu không biết cạnh không?
Không, phải biết ít nhất một cạnh để tính thể tích.
3. Làm sao chuyển từ cm³ sang m³ ?
Chia cho 1.000.000 (1 m³ =1.000.000 cm³ ).
4. Thể tích khối lập phương dùng để làm gì trong thực tế?
Tính khoang chứa, vật liệu xây dựng, thiết kế hộp hay sản phẩm cơ khí.
Thể tích là kiến thức cơ bản nhưng quan trọng. Việc nắm chắc công thức V=a³ , hiểu cách áp dụng, ví dụ minh họa và các mẹo sẽ giúp bạn:
Giải bài tập nhanh chóng
Tính toán vật liệu, khoang chứa chính xác
Thiết kế sản phẩm dạng khối dễ dàng
Khối lập phương cũng là nền tảng để học các hình khối 3D khác như hình hộp chữ nhật, hình trụ, hình cầu.
Bài viết này cung cấp đầy đủ thông tin từ khái niệm, công thức, ví dụ, mẹo, checklist và ứng dụng thực tế, giúp bạn nắm vững kiến thức và áp dụng linh hoạt.