Định lý pytago
Định lý Pythagoras là một định lý cơ bản trong hình học Euclid, phát biểu về mối quan hệ giữa ba cạnh của tam giác vuông. Định lý này được đặt theo tên nhà toán học Hy Lạp cổ đại Pythagoras (570 – 495 TCN), mặc dù các nền văn minh như Babylon và Ai Cập đã biết đến nguyên lý này từ trước.
Phát biểu định lý
Trong một tam giác vuông (tam giác có một góc bằng 90∘), bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông.
Công thức của định lý Pythagoras là:
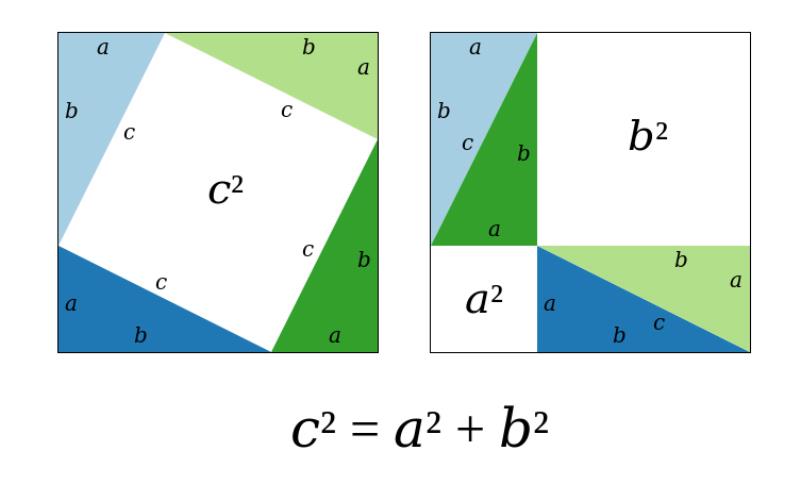
a² + b² = c²
Trong đó:
a và b là độ dài của hai cạnh góc vuông.
c là độ dài của cạnh huyền (cạnh đối diện góc vuông).
Ý nghĩa của công thức:
a² + b² = c² nói rằng tổng bình phương của hai cạnh góc vuông bằng bình phương của cạnh huyền. Đây là một định lý cơ bản trong hình học, giúp tính toán độ dài các cạnh trong tam giác vuông.
Định lý Pythagoras là gìĐịnh lý Pythagoras là một trong những định lý nền tảng của toán học, đặc biệt trong hình học và đại số. Tầm quan trọng của định lý này thể hiện qua nhiều khía cạnh, từ lý thuyết toán học đến các ứng dụng thực tiễn trong cuộc sống và khoa học. Dưới đây là một số lý do chính khiến định lý Pythagoras quan trọng:
Cơ sở của Hình học Euclid
Định lý Pythagoras là một nguyên tắc quan trọng trong hình học Euclid, giúp xác định mối quan hệ giữa ba cạnh của một tam giác vuông. Nó giúp chứng minh nhiều định lý khác trong hình học, như:
Tính chất của đường chéo hình chữ nhật
Khoảng cách giữa hai điểm trong hệ tọa độ
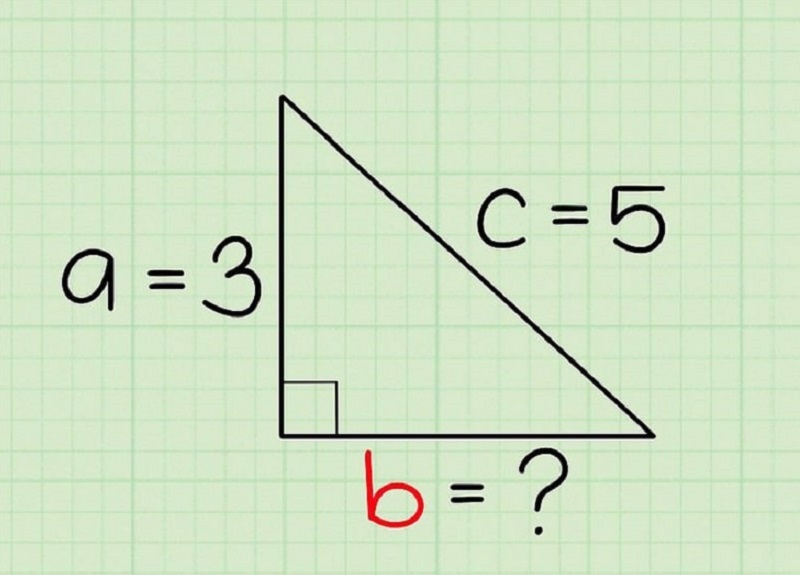Tại sao định lý Pythagoras lại quan trọngỨng dụng rộng rãi trong cuộc sống và kỹ thuật
a) Trong xây dựng và kiến trúc
Kỹ sư và kiến trúc sư sử dụng định lý Pythagoras để đo đạc, tính toán khoảng cách và thiết kế công trình.
Ví dụ: Khi cần xác định độ dài đường chéo của một bức tường, cầu thang, hoặc mái nhà, họ có thể sử dụng định lý này thay vì đo trực tiếp.
b) Trong bản đồ và hệ thống định vị GPS
Định lý Pythagoras giúp tính toán khoảng cách giữa hai điểm trên mặt phẳng, từ đó hỗ trợ trong hàng không, hàng hải, và hệ thống định vị toàn cầu (GPS).
Các vệ tinh GPS sử dụng công thức này để xác định vị trí chính xác của các vật thể trên Trái Đất.
c) Trong vật lý và thiên văn học
Các nhà khoa học sử dụng định lý này để tính toán khoảng cách giữa các thiên thể, đo quỹ đạo của hành tinh và xác định vị trí của các vì sao.
Trong cơ học, định lý Pythagoras giúp giải quyết các bài toán về vận tốc, lực và chuyển động theo hai phương vuông góc.
d) Trong đồ họa máy tính và trò chơi điện tử
Các nhà lập trình đồ họa sử dụng định lý Pythagoras để tính khoảng cách giữa các điểm, giúp xác định hướng di chuyển của nhân vật hoặc tạo hiệu ứng bóng đổ trong trò chơi.
Trong lập trình game 2D và 3D, nó giúp tạo ra hệ thống va chạm, hiệu ứng ánh sáng, và các phép biến đổi hình học.
e) Trong y học và sinh học
Định lý này được sử dụng để đo lường trong chẩn đoán hình ảnh y khoa, ví dụ như chụp X-quang và CT Scan để xác định vị trí chính xác của các cơ quan trong cơ thể.
Trong nghiên cứu sinh học, nó giúp tính toán quỹ đạo di chuyển của động vật, cũng như cấu trúc của ADN và protein.
Cơ sở cho nhiều ngành khoa học khác
Không chỉ quan trọng trong toán học, định lý Pythagoras còn là nền tảng cho nhiều lĩnh vực khác như:
Đại số và giải tích: Định lý này giúp chứng minh nhiều công thức trong hình học giải tích và lượng giác.
Khoa học dữ liệu và trí tuệ nhân tạo: Sử dụng để tính toán khoảng cách giữa các điểm dữ liệu trong các thuật toán machine learning.
Kinh tế và tài chính: Trong một số mô hình kinh tế, các công thức đo lường rủi ro và tối ưu hóa cũng có liên quan đến định lý này.
Đơn giản nhưng mạnh mẽ
Một trong những điều khiến định lý Pythagoras quan trọng là vì:
Nó có công thức đơn giản: c² = a² + b² , nhưng lại có ứng dụng cực kỳ rộng rãi.
Dễ hiểu, dễ áp dụng và có thể sử dụng trong nhiều tình huống khác nhau.
bài tập áp dụng định lý PythagoraDưới đây là một số bài tập từ cơ bản đến nâng cao giúp bạn luyện tập và áp dụng định lý Pythagoras:
Bài tập 1: Tính cạnh huyền của tam giác vuông
Một tam giác vuông có hai cạnh góc vuông lần lượt là 6 cm và 8 cm. Hãy tính độ dài cạnh huyền.
Lời giải:
Áp dụng định lý Pythagoras:
c² = a² + b² = 6² + 8² = 36+64=100
c= √100=10 cm
Đáp số: c=10 cm.
Bài tập 2: Tìm cạnh góc vuông
Cho một tam giác vuông có cạnh huyền dài 13 cm và một cạnh góc vuông dài 5 cm. Tìm cạnh góc vuông còn lại.
Lời giải:
Gọi cạnh góc vuông cần tìm là bbb, áp dụng định lý Pythagoras:
c² = a² + b²
13²=5²+b²
169=25+b²
b²= √144 =12 cm
Đáp số: b=12 cm.
Bài tập 3: Kiểm tra tam giác có phải tam giác vuông không?
Cho một tam giác có ba cạnh: 7 cm, 24 cm, 25 cm. Hãy kiểm tra xem tam giác này có phải là tam giác vuông không.
Lời giải:
Kiểm tra xem tổng bình phương hai cạnh nhỏ hơn có bằng bình phương cạnh lớn nhất không:
7²+24²=49+576=625
25²=625
Vì 7²+24²=25², nên tam giác này là tam giác vuông.
Đáp số: Đây là tam giác vuông.
Bài tập 4: Ứng dụng trong thực tế
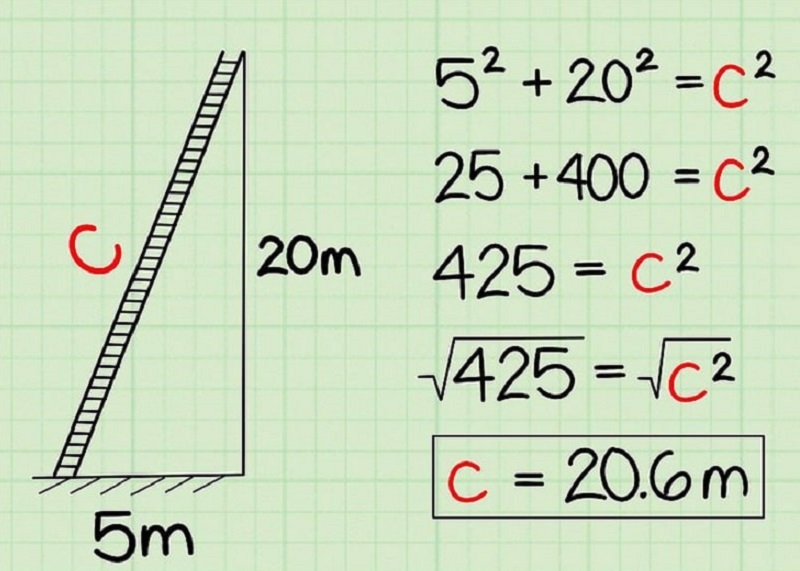
Một cái thang dài 10 m được đặt dựa vào một bức tường. Chân thang cách tường 6 m. Hỏi thang chạm vào tường ở độ cao bao nhiêu?
Lời giải:
Gọi độ cao cần tìm là hhh. Theo định lý Pythagoras:
10²=6²+h²
100=36+h²
h²=64
h= √64 = 8 m
Đáp số: h=8 m.
Bài tập 5: Tính đường chéo của hình chữ nhật
Một hình chữ nhật có chiều dài 9 cm và chiều rộng 12 cm. Tính độ dài đường chéo của hình chữ nhật.
Lời giải:
Đường chéo hình chữ nhật chia hình chữ nhật thành hai tam giác vuông, với hai cạnh góc vuông là 9 cm và 12 cm.
Áp dụng định lý Pythagoras:
d²=9²+12²
d²=81+144=225
d= √225=15 cm
Đáp số: Đường chéo dài 15 cm.
Các bài tập trên giúp bạn áp dụng định lý Pythagoras vào nhiều trường hợp khác nhau, từ tính cạnh tam giác đến ứng dụng thực tế như đo khoảng cách, xác định chiều cao hoặc đường chéo. Hãy thực hành thường xuyên để nắm vững cách sử dụng định lý này!
Ứng dụng của định lý PythagorasĐịnh lý Pythagoras không chỉ là một công cụ toán học lý thuyết mà còn có nhiều ứng dụng quan trọng trong thực tế. Từ xây dựng, kỹ thuật, khoa học đến đời sống hàng ngày, định lý này giúp con người tính toán khoảng cách, đo lường và giải quyết nhiều vấn đề thực tiễn.
Trong xây dựng và kiến trúc
Đo lường và thiết kế: Kiến trúc sư và kỹ sư xây dựng sử dụng định lý Pythagoras để tính toán độ dài, góc và kích thước trong thiết kế nhà cửa, cầu đường và công trình kiến trúc.
Kiểm tra góc vuông: Khi xây tường hoặc lát sàn, công nhân có thể dùng tam giác có tỉ lệ 3 - 4 - 5 (một tam giác vuông đặc biệt) để đảm bảo tường thẳng đứng và góc vuông chính xác.
Tính đường chéo: Khi cần xác định độ dài đường chéo của một căn phòng, một tấm ván hoặc một mảnh vải, người ta áp dụng định lý Pythagoras.
👉 Ví dụ: Một tấm ván hình chữ nhật có chiều dài 6m và chiều rộng 8m, vậy đường chéo sẽ là:
d²=6²+8²=36+64=100⇒d=√100=10m
Vậy đường chéo tấm ván dài 10m.
Trong hệ thống định vị GPS và bản đồ
Định lý Pythagoras được sử dụng để tính khoảng cách giữa hai điểm trên bản đồ bằng cách giả định khoảng cách đó tạo thành một cạnh huyền của tam giác vuông.
Hệ thống GPS (Global Positioning System) cũng dựa vào các phép tính toán theo định lý này để xác định khoảng cách giữa vệ tinh và người dùng.
👉 Ví dụ: Nếu một người di chuyển 3 km về phía đông và sau đó 4 km về phía bắc, khoảng cách thực tế mà họ di chuyển từ điểm ban đầu là:
d=√3²+√4²=√9+√16=√25=5km
Vậy họ cách vị trí ban đầu 5km theo đường thẳng.
Trong vật lý và thiên văn học
Tính toán quỹ đạo của thiên thể: Các nhà thiên văn học sử dụng định lý Pythagoras để tính khoảng cách giữa các hành tinh, sao và thiên thể trong vũ trụ.
Phân tích lực trong cơ học: Trong vật lý, lực thường được phân tích thành các thành phần vuông góc nhau. Định lý Pythagoras giúp tính độ lớn của lực tổng hợp khi hai lực tác động theo hai phương vuông góc.
👉 Ví dụ: Một vật thể chịu tác động của hai lực 6N theo phương ngang và 8N theo phương thẳng đứng, lực tổng hợp mà vật thể chịu là:
F=√6²+√8²=√36+√64=√100=10N
Vậy lực tổng hợp tác động lên vật là 10N.
Trong đồ họa máy tính và lập trình game
Định lý Pythagoras giúp lập trình viên tính khoảng cách giữa hai điểm trong không gian 2D và 3D, một yếu tố quan trọng trong đồ họa máy tính, game và hiệu ứng hình ảnh.
Dùng để xác định hướng di chuyển của nhân vật hoặc tạo hiệu ứng bóng đổ, ánh sáng trong game.
👉 Ví dụ: Trong một trò chơi, nếu một nhân vật đứng ở tọa độ (2,3) và cần di chuyển đến (6,8), khoảng cách di chuyển là:
d=√(6−2)²+√(8−3)²=√16+√25=√41≈6.4
Vậy nhân vật cần di chuyển khoảng 6.4 đơn vị.
Trong y học và sinh học
Hình ảnh y khoa: Định lý Pythagoras được sử dụng trong chụp X-quang, CT Scan, MRI để xác định khoảng cách giữa các cơ quan nội tạng hoặc vị trí tổn thương trong cơ thể.
Phân tích cử động cơ thể: Các nhà khoa học sử dụng định lý này để nghiên cứu chuyển động của con người và động vật, đặc biệt trong thiết kế chân tay giả.
Trong hàng không và hải quân
Tính quãng đường bay: Máy bay thường bay theo đường chéo trên bản đồ, và định lý Pythagoras giúp phi công tính toán chính xác quãng đường thực sự.
Định vị tàu thuyền: Tương tự, hải quân sử dụng định lý này để xác định khoảng cách giữa tàu và bờ biển hoặc giữa các tàu với nhau.
👉 Ví dụ: Một máy bay bay 300 km về phía bắc và sau đó 400 km về phía đông, khoảng cách thực tế máy bay đã bay là:
d= √300²+√400²=√90000+√160000=√250000=500km
Vậy máy bay đã di chuyển 500km theo đường thẳng.
Trong thể thao
Định lý Pythagoras được sử dụng trong các môn thể thao như bóng rổ, bóng đá, bóng chày để tính toán quỹ đạo và khoảng cách.
Ví dụ, trong bóng chày, nếu một cầu thủ ném bóng từ gôn nhà đến gôn thứ hai, người ta có thể dùng định lý này để tính khoảng cách trực tiếp.
Định lý Pythagoras không chỉ là một định lý toán học mà còn là một công cụ mạnh mẽ có mặt trong nhiều lĩnh vực của đời sống. Từ xây dựng, khoa học, kỹ thuật đến y học và trí tuệ nhân tạo, định lý này đóng vai trò quan trọng trong việc tính toán khoảng cách, đo lường và thiết kế. Nhờ có định lý Pythagoras, con người có thể hiểu rõ hơn về thế giới xung quanh và phát triển những công nghệ tiên tiến phục vụ đời sống.
Qua bài viết trên, Nhà Hàng bếp khói đã cùng bạn tìm hiểu rõ về định lý Pythagoras, một trong những định lý cơ bản và quan trọng nhất trong toán học. Định lý này không chỉ giúp giải quyết các bài toán hình học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực thực tế. Việc nắm vững và áp dụng định lý Pythagoras không chỉ giúp chúng ta củng cố kiến thức toán học mà còn mở ra khả năng giải quyết các vấn đề trong đời sống và khoa học.