Định lý pytago
Định lý Pythagoras là một định lý trong hình học, áp dụng cho tam giác vuông. Định lý này phát biểu rằng: Bình phương của cạnh huyền (cạnh đối diện góc vuông) bằng tổng bình phương của hai cạnh góc vuông.
Công thức của định lý Pythagoras là:
a² + b² = c²
Trong đó:
a và b là độ dài của hai cạnh góc vuông.
c là độ dài của cạnh huyền (cạnh đối diện góc vuông).
Ý nghĩa của công thức:
a² + b² = c² nói rằng tổng bình phương của hai cạnh góc vuông bằng bình phương của cạnh huyền. Đây là một định lý cơ bản trong hình học, giúp tính toán độ dài các cạnh trong tam giác vuông.
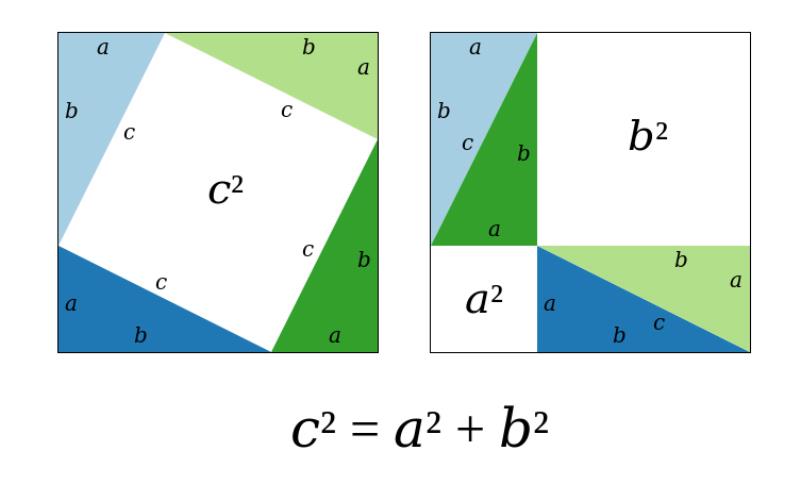Công thức của định lý PythagorasĐịnh lý Pythagoras là một trong những định lý cơ bản và quan trọng nhất trong toán học vì những lý do sau:
- Cơ sở của hình học Euclid: Định lý Pythagoras là nền tảng của hình học Euclid, nơi các định lý và công thức hình học được xây dựng trên cơ sở của tam giác vuông. Điều này giúp phát triển lý thuyết về không gian và các hình học phức tạp hơn.
- Ứng dụng trong nhiều lĩnh vực: Định lý này không chỉ có giá trị lý thuyết mà còn có ứng dụng rộng rãi trong nhiều ngành nghề như xây dựng, kỹ thuật, vật lý, đo đạc, hàng không, và địa lý. Ví dụ, trong khảo sát đất đai, việc tính khoảng cách giữa hai điểm, đo độ cao của các tòa nhà, hay xác định độ nghiêng của mặt đất đều có thể áp dụng định lý Pythagoras.
- Công cụ giải quyết vấn đề: Định lý Pythagoras cung cấp một công cụ mạnh mẽ để giải quyết các bài toán hình học, đặc biệt là các bài toán liên quan đến tam giác vuông. Việc áp dụng định lý giúp giải quyết nhiều bài toán về độ dài của các cạnh trong tam giác vuông, làm nền tảng cho các công thức và lý thuyết toán học khác.
- Kết nối với các lý thuyết toán học khác: Định lý Pythagoras là cầu nối giữa đại số và hình học, giúp học sinh và sinh viên hiểu được mối quan hệ giữa các phép toán và hình vẽ. Nó là một phần quan trọng trong việc học các chủ đề khác, như lượng giác, vectơ, và không gian ba chiều.
- Chứng minh tính đúng đắn của nhiều công thức khác: Định lý Pythagoras là cơ sở để chứng minh các công thức trong toán học, chẳng hạn như công thức về khoảng cách giữa hai điểm trong không gian hai chiều, hoặc công thức Pythagoras mở rộng trong không gian ba chiều.
Tại sao định lý Pythagoras lại quan trọng trong toán học?Định lý Pythagoras áp dụng khi có một tam giác vuông, tức là tam giác có một góc vuông (90 độ). Cụ thể, định lý này chỉ có hiệu lực khi:
- Có một góc vuông trong tam giác, nghĩa là một trong ba góc của tam giác bằng 90 độ.
- Bạn có thể áp dụng công thức a² + b² = c² để tính toán độ dài các cạnh của tam giác vuông, trong đó:
- a và b là độ dài của hai cạnh góc vuông.
- c là độ dài của cạnh huyền (cạnh đối diện góc vuông).
Vì vậy, nếu không có góc vuông trong tam giác, định lý Pythagoras không thể áp dụng được.
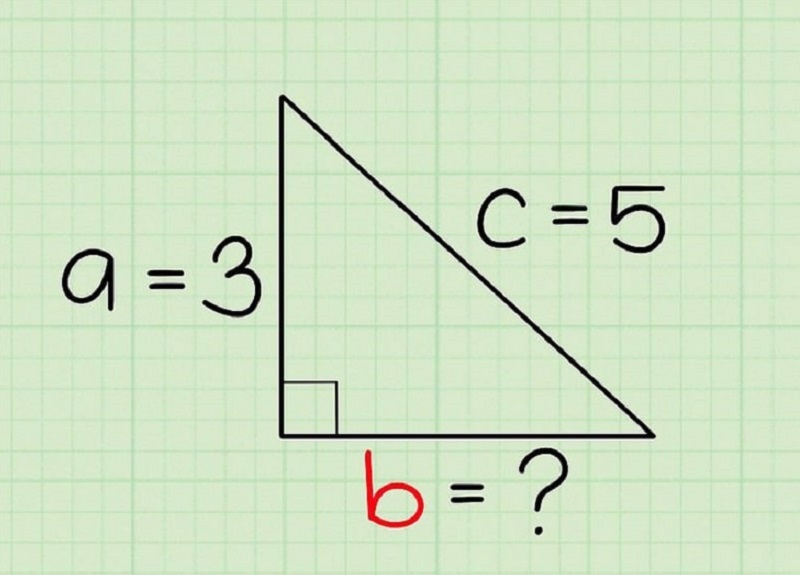Định lý pytago áp dụng khi nào?Để sử dụng định lý Pythagoras tính cạnh của tam giác vuông, bạn cần áp dụng công thức:
a² + b² = c²
Trong đó:
a và b là độ dài của hai cạnh góc vuông.
c là độ dài của cạnh huyền (cạnh đối diện góc vuông).
Cách tính cạnh trong tam giác vuông:
Tính cạnh huyền (c) khi biết hai cạnh góc vuông (a và b):
Công thức:
c = √(a² + b²)
Ví dụ: Nếu a=3 b=4b = 4b=4, thì: c = √(3² + 4²) = √(9 + 16) = √25 = 5
Tính một cạnh góc vuông (a hoặc b) khi biết cạnh huyền (c) và một cạnh góc vuông còn lại:
Nếu bạn muốn tính cạnh góc vuông aaa, khi biết cạnh huyền ccc và cạnh góc vuông bbb, công thức sẽ là:
a = √(c² - b²)
Ví dụ: Nếu c=5 và b=4 thì: a = √(5² - 4²) = √(25 - 16) = √9 = 3 Vậy cạnh góc vuông a=3.
Lưu ý:
Định lý Pythagoras chỉ áp dụng cho tam giác vuông, tức là tam giác có một góc bằng 90 độ.
Khi áp dụng công thức, luôn phải chắc chắn rằng bạn đang làm việc với tam giác vuông để công thức có giá trị chính xác.
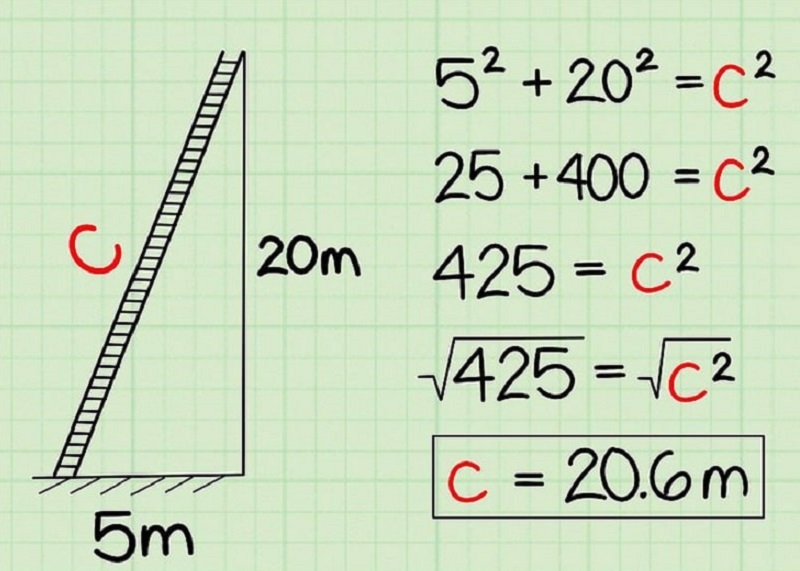Cách sử dụng định lý Pythagoras để tính cạnh của tam giác vuôngĐịnh lý Pytago có nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực liên quan đến hình học, đo đạc, và xây dựng. Dưới đây là một số ứng dụng phổ biến:
Xây dựng và kiến trúc:
Định lý Pythagoras giúp xác định độ nghiêng của mái nhà, chiều cao của tòa nhà, hay khoảng cách giữa hai điểm trong xây dựng.
Trong việc dựng các công trình vuông góc, người kỹ sư sử dụng định lý này để đảm bảo các góc vuông chính xác.
Định vị và đo đạc:
Định lý Pythagoras được sử dụng trong đo đạc để tính toán khoảng cách giữa hai điểm trong không gian hai chiều (hoặc ba chiều). Ví dụ, trong đo đạc đất đai hoặc khi vẽ bản đồ.
Khi bạn biết khoảng cách theo chiều ngang và chiều dọc, bạn có thể sử dụng định lý để tính khoảng cách chéo (ví dụ trong việc đo chiều dài của một đường chéo của mảnh đất hình chữ nhật).
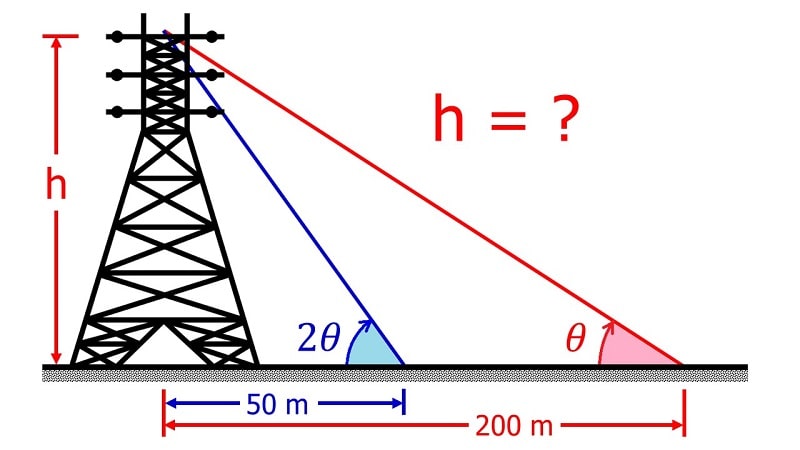Định lý Pythagoras có ứng dụng gì trong thực tế?Hệ thống GPS:
Trong công nghệ định vị toàn cầu (GPS), định lý Pythagoras giúp tính toán khoảng cách giữa các điểm trên bề mặt Trái Đất, từ đó xác định vị trí chính xác.
Thiết kế đồ họa:
Trong thiết kế đồ họa và lập trình, định lý Pythagoras được sử dụng để tính khoảng cách giữa hai điểm trong không gian hai chiều, ví dụ như khi vẽ các hình ảnh, tính toán độ dài các đoạn thẳng trong các phần mềm CAD.
Vật lý:
Định lý Pythagoras cũng được áp dụng trong nhiều lĩnh vực vật lý, ví dụ như trong tính toán vận tốc tổng hợp, nơi các vận tốc chuyển động theo các hướng khác nhau có thể được tính bằng cách áp dụng định lý Pythagoras.
Giải quyết các bài toán trong thể thao:
Trong các môn thể thao như bóng rổ, bóng đá, hoặc đua xe, định lý Pythagoras giúp tính toán khoảng cách hoặc xác định điểm đến của bóng.
Với những ứng dụng này, định lý Pythagoras là công cụ hữu ích giúp giải quyết nhiều bài toán trong đời sống hàng ngày, đặc biệt là khi cần tính toán các khoảng cách trong không gian hai chiều hoặc ba chiều.
Qua bài viết trên, Nhà Hàng bếp khói đã cùng bạn tìm hiểu rõ về định lý Pythagoras, một trong những định lý cơ bản và quan trọng nhất trong toán học. Định lý này không chỉ giúp giải quyết các bài toán hình học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực thực tế. Việc nắm vững và áp dụng định lý Pythagoras không chỉ giúp chúng ta củng cố kiến thức toán học mà còn mở ra khả năng giải quyết các vấn đề trong đời sống và khoa học.