Thể tích khối lập phương
Thể tích của khối lập phương là không gian mà khối lập phương chiếm trong ba chiều. Nó được tính bằng cách lấy độ dài của một cạnh của khối lập phương rồi nâng lên lũy thừa ba.
Công thức tính thể tích của khối lập phương là:
V = a³
Trong đó:
- V là thể tích của khối lập phương.
- a là độ dài của một cạnh của khối lập phương.
Khối lập phương là một hình dạng ba chiều với tất cả các mặt đều là hình vuông và các cạnh đều có độ dài bằng nhau. Vì vậy, thể tích của khối lập phương chỉ phụ thuộc vào độ dài của cạnh.

Hình lập phương là gì?Để tính thể tích của khối lập phương, bạn cần biết độ dài của một cạnh. Công thức tính thể tích của khối lập phương rất đơn giản:
V = a³
Trong đó:
- V là thể tích của khối lập phương.
- a là độ dài của một cạnh của khối lập phương.
Các bước tính thể tích của khối lập phương:
- Xác định độ dài của một cạnh (a).
- Áp dụng công thức: Lấy độ dài cạnh aaa nâng lên lũy thừa ba (a³).
- Kết quả sẽ là thể tích của khối lập phương.
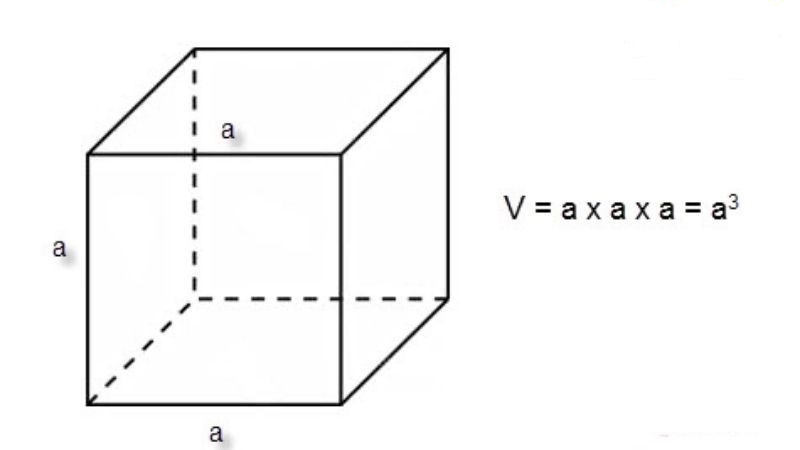
Công thức tính thể tích của khối lập phươngVí dụ về tính thể tích:
- Giả sử bạn có một khối lập phương có độ dài cạnh là 5 cm, bạn sẽ tính thể tích như sau:
- V = 4³ = 4 × 4 × 4 = 64 cm³.
- Vậy thể tích của khối lập phương này là 125 cm³.
Bài tập ứng dụng về thể tích của khối lập phương:
Bài tập 1:
Một khối lập phương có độ dài cạnh là 8 cm. Tính thể tích của khối lập phương này.
Giải: Áp dụng công thức tính thể tích:
V = 8³ = 8 × 8 × 8 = 512 cm³.
Đáp án: Thể tích của khối lập phương là 512 cm³.
Bài tập 2:
Khối lập phương có thể tích là 1000 cm³. Tính độ dài cạnh của khối lập phương.
Giải: Vì thể tích của khối lập phương được tính theo công thức V = a³, nên để tìm độ dài cạnh a, bạn cần lấy căn bậc ba của thể tích:
a = ∛1000 = 10 cm.

Các bài toán áp dụngBài tập 3:
Một hộp quà có dạng khối lập phương với độ dài cạnh là 12 cm. Bạn cần đóng gói 5000 cm³ quà vào trong hộp này. Hỏi liệu khối lập phương này có thể chứa hết quà hay không?
Giải: Tính thể tích của khối lập phương:
V = 12³ = 12 × 12 × 12 = 1728 cm³.
Vì thể tích của khối lập phương (1728 cm³) nhỏ hơn thể tích quà (5000 cm³), khối lập phương này không đủ để chứa hết quà.
Thể tích của khối lập phương thay đổi theo một cách rất đặc biệt khi độ dài cạnh thay đổi. Cụ thể, thể tích của khối lập phương tỉ lệ với lũy thừa ba của độ dài cạnh. Điều này có nghĩa là:
- Nếu độ dài cạnh của khối lập phương tăng lên, thể tích sẽ tăng gấp ba lần theo mỗi đơn vị tăng của cạnh.
- Nếu độ dài cạnh giảm xuống, thể tích cũng sẽ giảm theo lũy thừa ba.
Công thức tính thể tích của khối lập phương là:
Trong đó:
- V là thể tích của khối lập phương.
- a là độ dài của một cạnh của khối lập phương.
Ví dụ minh họa:
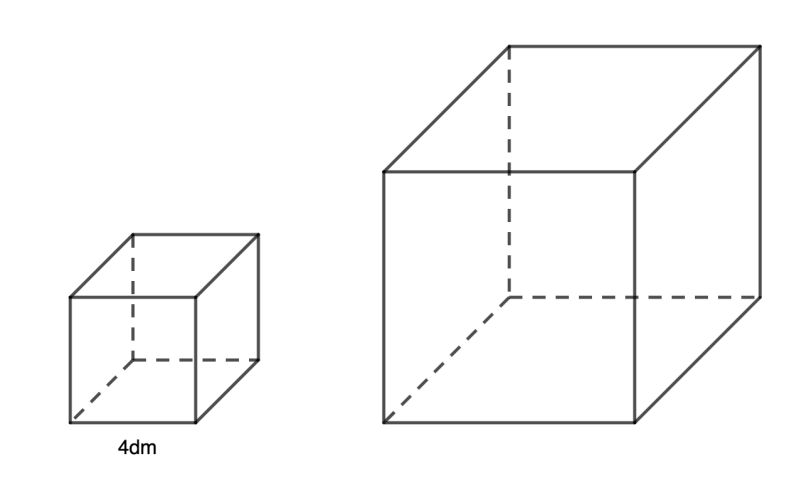
Ví dụ minh hoạNếu độ dài cạnh tăng gấp đôi:
- Giả sử ban đầu độ dài cạnh là a=3 cm. Thể tích sẽ là: V = 3³ = 3 × 3 × 3 = 27 cm³.
- Nếu độ dài cạnh tăng lên gấp đôi (tức là a=6 cm), thể tích sẽ là: V = 6³ = 6 × 6 × 6 = 216 cm³.
- So sánh: Thể tích tăng gấp 8 lần, vì 2³ = 8.
Nếu độ dài cạnh giảm đi một nửa:
- Giả sử độ dài cạnh ban đầu là a=4 cm. Thể tích là: V = 4³ = 4 × 4 × 4 = 64 cm³.
- Nếu cạnh giảm xuống một nửa (tức là a=2 cm), thể tích sẽ là: V = 2³ = 2 × 2 × 2 = 8 cm³.
- So sánh: Thể tích giảm đi 8 lần, vì (1/2)³ = 1/8.
Do đó:
- Thể tích của khối lập phương thay đổi mạnh mẽ khi độ dài cạnh thay đổi, theo lũy thừa ba của cạnh.
- Khi cạnh tăng, thể tích tăng theo lũy thừa ba của sự thay đổi.
- Khi cạnh giảm, thể tích giảm theo lũy thừa ba.
Thể tích của khối lập phương trong thực tế có thể được áp dụng vào rất nhiều tình huống khác nhau. Khối lập phương là một hình khối có tất cả các cạnh bằng nhau và mỗi mặt là một hình vuông. Do đó, thể tích của khối lập phương có thể giúp chúng ta tính toán không gian mà khối này chiếm trong thực tế.
Ứng dụng của thể tích của khối lập phương trong thực tế:
Tính toán dung tích các vật dụng hình khối lập phương: Nếu bạn có một hộp quà, thùng chứa hoặc khối kim loại có dạng khối lập phương, thể tích sẽ giúp bạn biết được không gian mà vật thể đó chiếm. Ví dụ, bạn có thể tính xem thùng chứa này chứa được bao nhiêu lít nước, hoặc bao nhiêu khối vật liệu có thể được đựng trong đó.
Ví dụ: Một thùng hình khối lập phương có cạnh dài 5 cm, thể tích sẽ là:
V = 5³ = 5 × 5 × 5 = 125 cm³.
Điều này có thể cho bạn biết được số lượng vật liệu hay dung tích của thùng chứa.
- Kiến trúc và xây dựng: Trong xây dựng, các khối vật liệu như gạch, đá có thể có dạng hình lập phương. Để tính toán số lượng vật liệu cần thiết cho một dự án xây dựng, bạn sẽ cần biết thể tích của các khối vật liệu này.
- Chế tạo các đồ vật: Đối với các nhà sản xuất hoặc thợ thủ công, thể tích của các vật dụng, sản phẩm (như hộp đựng đồ, khối kim loại, khối gỗ) là yếu tố quan trọng để tính toán nguyên vật liệu cần thiết hoặc để dự đoán trọng lượng của sản phẩm.
- Tính toán không gian trong các vật dụng: Nếu bạn mua một chiếc hộp, tủ, hoặc bất kỳ vật dụng nào có dạng khối lập phương (hoặc gần như khối lập phương), thể tích sẽ cho bạn biết không gian chứa đựng đồ đạc bên trong là bao nhiêu.
- Ứng dụng trong vật lý: Thể tích của khối lập phương cũng xuất hiện trong các bài toán vật lý, đặc biệt là trong tính toán không gian hoặc khối lượng của các vật thể hình khối lập phương. Việc tính toán này có thể dùng để xác định lượng chất lỏng cần chứa trong một thùng hoặc thể tích không gian mà một vật thể chiếm.
Ví dụ ứng dụng thực tế:
Ví dụ 1: Tính thể tích của một thùng chứa nước
Một thùng chứa nước có dạng khối lập phương, với mỗi cạnh dài 1 m (100 cm). Bạn muốn biết thùng này chứa được bao nhiêu lít nước.
Giải: Thể tích của thùng là:
V = 100³ = 100 × 100 × 100 = 1,000,000 cm³.
Vì 1 lít = 1000 cm³, nên:
1,000,000 cm³ = 1000 lít.
Đáp án: Thùng chứa được 1000 lít nước.
Ví dụ 2: Tính thể tích một khối gỗ
Một khối gỗ có dạng khối lập phương với độ dài cạnh là 2 m. Bạn muốn biết thể tích của khối gỗ này để xác định trọng lượng hoặc lượng gỗ cần để cắt ra.
Giải: Thể tích của khối gỗ là:
V = 2³ = 2 × 2 × 2 = 8 m³.
Đáp án: Thể tích khối gỗ là 8 m³.
Qua bài viết này, chúng ta đã hiểu rõ hơn về cách tính thể tích của khối lập phương và tầm quan trọng của nó trong toán học cũng như trong cuộc sống thực tế. Việc áp dụng công thức để tính thể tích giúp giải quyết nhiều bài toán đơn giản và phức tạp, từ việc tính toán không gian chứa đựng đến ứng dụng trong thiết kế và sản xuất. Hy vọng rằng bài viết của Nhà Hàng bếp khói đã giúp bạn nắm vững kiến thức về thể tích của khối lập phương và biết cách áp dụng nó vào các tình huống thực tế một cách hiệu quả.>> Xem thêm: Địa điểm tổ chức sinh nhật công ty